What Number Should Be Added To The Expression X2+2x To Change It Into A Perfect Square Trinomial?

Quadratic Equations

Solving equations is the central theme of algebra. All skills learned pb eventually to the power to solve equations and simplify the solutions. In previous capacity nosotros have solved equations of the first caste. Y'all at present have the necessary skills to solve equations of the 2d caste, which are known every bit quadratic equations.

QUADRATICS SOLVED Past FACTORING

OBJECTIVES

Upon completing this department y'all should be able to:

1. Identify a quadratic equation.
2. Identify a quadratic equation in standard form.
3. Solve a quadratic equation by factoring.

A quadratic equation is a polynomial equation that contains the 2d degree, only no college degree, of the variable.

The standard form of a quadratic equation is axⁱⁱ + bx + c = 0 when a ≠ 0 and a, b, and c are real numbers.

All quadratic equations tin be put in standard form, and whatever equation that tin can be put in standard form is a quadratic equation. In other words, the standard class represents all quadratic equations.

The solution to an equation is sometimes referred to as the root of the equation.

This theorem is proved in most college algebra books.

An important theorem, which cannot be proved at the level of this text, states "Every polynomial equation of degree n has exactly n roots." Using this fact tells us that quadratic equations will ever accept ii solutions. It is possible that the 2 solutions are equal.

A quadratic equation will accept ii solutions because it is of degree two.

The simplest method of solving quadratics is past factoring. This method cannot always be used, because not all polynomials are factorable, but it is used whenever factoring is possible.

The method of solving by factoring is based on a simple theorem.

If AB = 0, then either A = 0 or B = 0.

In other words, if the product of ii factors is zero, then at to the lowest degree one of the factors is zero.

Nosotros will not attempt to prove this theorem simply notation carefully what it states. We can never multiply two numbers and obtain an answer of zero unless at least one of the numbers is aught. Of course, both of the numbers can exist zero since (0)(0) = 0.

Solution Step 1 Put the equation in standard course.

We must subtract half dozen from both sides.

Pace ii Factor completely.

Remember how to gene trinomials.

Step 3 Set up each factor equal to zero and solve for x. Since we have (x - 6)(x + i) = 0, we know that ten - vi = 0 or x + 1 = 0, in which case x = 6 or ten = - 1.

This applies the higher up theorem, which says that at least ane of the factors must have a value of zero.

Footstep iv Check the solution in the original equation. If 10 = vi, and so ten² - 5x = six becomes

Checking your solutions is a sure way to tell if you have solved the equation correctly.

Therefore, x = 6 is a solution. If ten = - ane, then x² - 5x = 6 becomes

Therefore, - 1 is a solution.

The solutions can be indicated either by writing x = 6 and ten = - ane or by using set notation and writing {six, - 1}, which we read "the solution set for x is 6 and - ane." In this text we volition use set notation.

In this example 6 and -1 are called the elements of the set.

Notation in this case that the equation is already in standard form.

Again, checking the solutions volition assure you that you did non make an error in solving the equation.
are besides called roots of the equation.

(x + one) is the to the lowest degree common denominator of all the fractions in the equation.
Remember, every term of the equation must be multiplied past (10 + one).

Cheque the solutions in the original equation.

Bank check in the original equation to brand sure y'all exercise not obtain a denominator with a value of cypher.

Notice hither the two solutions are equal. This only occurs when the trinomial is a perfect square.

INCOMPLETE QUADRATICS

OBJECTIVES

Upon completing this department you should be able to:

1. Identify an incomplete quadratic equation.
2. Solve an incomplete quadratic equation.

If, when an equation is placed in standard grade ax² + bx + c = 0, either b = 0 or c = 0, the equation is an incomplete quadratic.

Instance 1

5x² - ten = 0 is an incomplete quadratic, since the center term is missing and therefore b = 0.

When y'all meet an incomplete quadratic with c - 0 (third term missing), it can nevertheless be solved by factoring.

ten is a mutual factor. The product of two factors is zero. Nosotros therefore employ the theorem from the previous section.
Check these solutions.

Notice that if the c term is missing, you can ever gene x from the other terms. This means that in all such equations, zero will be ane of the solutions.
An incomplete quadratic with the b term missing must be solved by another method, since factoring will be possible but in special cases.

Example three Solve for x if ten² - 12 = 0.

Solution Since 10ⁱⁱ - 12 has no common factor and is not the divergence of squares, information technology cannot be factored into rational factors. But, from previous observations, we have the following theorem.

Note that there are 2 values that when squared volition equal A.

Using this theorem, we have

Bank check these solutions.

Add 10 to each side. Check these solutions.

Here 7x is a common gene. Check these solutions.

Note that in this case nosotros accept the foursquare of a number equal to a negative number. This can never be true in the real number system and, therefore, we take no existent solution.

COMPLETING THE Foursquare

OBJECTIVES

Upon completing this section you should be able to:

1. Identify a perfect foursquare trinomial.
2. Complete the third term to make a perfect square trinomial.
3. Solve a quadratic equation past completing the foursquare.

From your feel in factoring you already realize that not all polynomials are factorable. Therefore, nosotros need a method for solving quadratics that are not factorable. The method needed is called "completing the foursquare."

Offset let usa review the meaning of "perfect square trinomial." When nosotros square a binomial we obtain a perfect square trinomial. The general form is (a + b)ⁱⁱ = a^two + 2ab + b².

Remember, squaring a binomial means multiplying it by itself.

From the general form and these examples we tin can make the following observations concerning a perfect foursquare trinomial.

1. Two of the iii terms are perfect squares. 4x² and 9 in the kickoff example, 25x² and 16 in the 2d example, and a² and b² in the full general form.
   

   In other words, the first and third terms are perfect squares.

2. The other term is either plus or minus two times the product of the square roots of the other two terms.

The -7 term immediately says this cannot exist a perfect square trinomial. The task in completing the square is to notice a number to replace the -vii such that at that place will be a perfect square.

Consider this problem: Make full in the blank then that "xⁱⁱ + 6x + _______" will be a perfect square trinomial. From the two conditions for a perfect foursquare trinomial nosotros know that the blank must comprise a perfect square and that 6x must exist twice the product of the square root of 10² and the number in the blank. Since ten is already present in 6x and is a foursquare root of x², and so six must be twice the square root of the number we place in the blank. In other words, if we first take half of half dozen and then square that consequence, we will obtain the necessary number for the blank.

Therefore xⁱⁱ + 6x + 9 is a perfect square trinomial.

Now let's consider how we can use completing the square to solve quadratic equations.

Example 5 Solve xⁱⁱ + 6x - 7 = 0 past completing the square.

Recall that instead of -7, a +9 would brand the expression a perfect square.

Solution First nosotros detect that the -7 term must be replaced if nosotros are to have a perfect foursquare trinomial, and so we will rewrite the equation, leaving a blank for the needed number.

At this point, be careful not to violate whatever rules of algebra. For example, note that the 2nd form came from adding +7 to both sides of the equation. Never add something to one side without adding the aforementioned thing to the other side.

Now we find half of 6 = three and 3² = nine, to give us the number for the blank. Again, if we place a 9 in the blank we must also add ix to the right side equally well.

Recollect, if nine is added to the left side of the equation, it must also exist added to the right side.

Now factor the perfect square trinomial, which gives

Now x² + 6x + 9 may be written every bit (x + 3)².

Thus, ane and -seven are solutions or roots of the equation.

Case half-dozen Solve 2x² + 12x - 4 = 0 past completing the square.

Solution This trouble brings in some other difficulty. The first term, 2x², is not a perfect square.
We will right this by dividing all terms of the equation by 2 and obtain

In other words, obtain a coefficient of 1 for the 10^two term.

We now add 2 to both sides, giving

Again, this is more curtailed.

Instance seven Solve 3x² + 7x - ix = 0 by completing the square.

Solution Step 1 Split up all terms by three.

Again, obtain a coefficient of 1 for ten² by dividing past iii.

Step ii Rewrite the equation, leaving a blank for the term necessary to complete the square.

Step 3 Discover the square of one-half of the coefficient of x and add together to both sides.

It looks circuitous, but we are following the same exact rules every bit before.

Pace 4 Factor the completed square.

The factoring should never be a problem since we know we accept a perfect square trinomial, which ways nosotros find the square roots of the first and tertiary terms and use the sign of the middle term.

Yous should review the arithmetic involved in calculation the numbers on the right at this time if you lot have any difficulty.
We at present have

Step five Accept the square root of each side of the equation.

Stride half-dozen Solve for ten (two values).

Follow the steps in the previous computation and then note specially the last ine. What is the conclusion when the square of a quantity is equal to a negative number? "No real solution."

What real number can we square and obtain -7?

In summary, to solve a quadratic equation by completing the square, follow this step-by-stride method.

Step one If the coefficient of x2 is non 1, split up all terms past that coefficient.
Stride 2 Rewrite the equation in the form of x2 + bx + _______ = c + _______.
Footstep 3 Find the square of one-one-half of the coefficient of the ten term and add together this quantity to both sides of the equation.
Step 4 Factor the completed square and combine the numbers on the right-hand side of the equation.
Step five Discover the square root of each side of the equation.
Step 6 Solve for x and simplify.
If step 5 is not possible, then the equation has no existent solution.

These steps will help in solving the equations in the post-obit exercise.

THE QUADRATIC FORMULA

OBJECTIVES

Upon completing this section yous should be able to:

1. Solve the full general quadratic equation by completing the square.
2. Solve whatsoever quadratic equation past using the quadratic formula.
3. Solve a quadratic equation by completing the square.

The standard form of a quadratic equation is ax^two + bx + c = 0. This means that every quadratic equation can be put in this course. In a sense and so ax² + bx + c = 0 represents all quadratics. If you tin solve this equation, you will have the solution to all quadratic equations.

We will solve the general quadratic equation past the method of completing the square.

This is to obtain an xⁱⁱ term with a coefficient of 1.
This we did in the previous department many times.

Nosotros must add together to each side.

This course is called the quadratic formula and represents the solution to all quadratic equations.

Memorize this expression.

To utilize the quadratic formula you must place a, b, and c. To do this the given equation must always be placed in standard course.

Carefully substitute the values of a, b, and c in the formula.

Not every quadratic equation will take a real solution.

This equation is already in standard course.

At that place is no real solution since -47 has no real square root.

Again, this equation is in standard course.

This solution should now be simplified.

Word Issues

OBJECTIVES

Upon completing this department you should be able to:

1. Identify word problems that require a quadratic equation for their solution.
2. Solve word bug involving quadratic equations.

Certain types of word problems can exist solved by quadratic equations. The process of outlining and setting upward the problem is the same as taught in chapter 5, simply with problems solved by quadratics y'all must exist very careful to bank check the solutions in the problem itself. The physical restrictions within the problem tin eliminate 1 or both of the solutions.

Example 1 If the length of a rectangle is 1 unit more than twice the width, and the area is 55 square units, find the length and width.

Solution The formula for the area of a rectangle is Area = Length X Width. Let ten = width, 2x + i = length.

If x represents the width, then 2x represents twice the width and 2x + 1 represents 1 more than twice the width.

Place the quadratic equation in standard course.
This quadratic tin can exist solved by factoring.

At this point, you lot can run into that the solution x = -11/2 is not valid since 10 represents a measurement of the width and negative numbers are not used for such measurements. Therefore, the solution is

width = x = 5, length = 2x + 1 = 11.

A measurement cannot be a negative value.

The reciprocal of x is .
Remember LCD means everyman common denominator.
Every term must be multiplied by 10x.
Again, this quadratic can be factored.

Both solutions check. Therefore, the solution set is .

There are two solutions to this problem.

Instance 3 If a certain integer is subtracted from half dozen times its square, the event is 15. Observe the integer.

Solution Let x = the integer. And then

Since neither solution is an integer, the problem has no solution.

You might exist tempted to give these values equally a solution unless you paid shut attention to the fact that the trouble asked for an integer.

Example 4 A subcontract manager has 200 meters of fence on hand and wishes to enclose a rectangular field so that it volition comprise 2,400 foursquare meters in expanse. What should the dimensions of the field be?

Solution Here there are 2 formulas involved. P = 2l + 2w for the perimeter and A = lw for the surface area.
Offset using P = 2l + 2w, nosotros become

Nosotros can now utilize the formula A = lw and substitute (100 - l) for w, giving

The field must be 40 meters wide past 60 meters long.

We could but too solve for l obtaining l = 100 - westward. Then

Annotation that in this problem we actually utilize a organization of equations

P = 2 fifty + 2 west
A = 50 w.

In general, a system of equations in which a quadratic is involved volition be solved by the exchange method. (See affiliate vi.)

SUMMARY

Key Words

• A quadratic equation is a polynomial equation in one unknown that contains the 2nd degree, but no higher degree, of the variable.
• The standard form of a quadratic equation is axⁱⁱ + bx + c = 0, when a ≠ 0.
• An incomplete quadratic equation is of the grade ax² + bx + c = 0, and either b = 0 or c = 0.
• The quadratic formula is
  

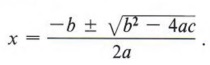
Procedures

• The most direct and more often than not easiest method of finding the solutions to a quadratic equation is factoring. This method is based on the theorem: if AB = 0, so A = 0 or B = 0. To use this theorem we put the equation in standard grade, gene, and gear up each factor equal to zero.
• To solve a quadratic equation by completing the square, follow these steps:
  Step one If the coefficient of 10² is not 1, divide all terms by that coefficient.
  Step 2 Rewrite the equation in the form of x² + bx +_____ = c + _____
  Step iii Find the square of half of the coefficient of the x term and add together this quantity to both sides of the equation.
  Step 4 Factor the completed square and combine the numbers on the right-hand side of the equation.
  Step 5 Find the foursquare root of each side of the equation.
  Stride 6 Solve for ten and simplify.
• The method of completing the foursquare is used to derive the quadratic formula.
• To use the quadratic formula write the equation in standard form, identify a, b, and c, and substitute these values into the formula. All solutions should be simplified.

Source: https://quickmath.com/webMathematica3/quickmath/equations/quadratics/basic.jsp

Posted by: garrettwilicaut.blogspot.com

Share this post